​Тригонометрические выражения. Преобразование тригонометрических выражений

Тригонометрические функции имеют широкое применение. Множество физических процессов описывается ими: колебания различной природы, волны. С их помощью проводятся технические расчёты, как фигур различного очертания, так и нагрузок на определённые детали механизмов. Соотношения тригонометрических функций с искомыми неизвестными величинами под их знаком представляют тригонометрические выражения.

Для результативной работы с выражениями в алгебре существуют многочисленные формулы, позволяющие упрощать их.

Основные тригонометрические тождества в основе представляют теорему Пифагора для треугольника, остальные формулы определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Запомнить их поможет подсказка: они взаимосвязаны и определённым образом симметричны.

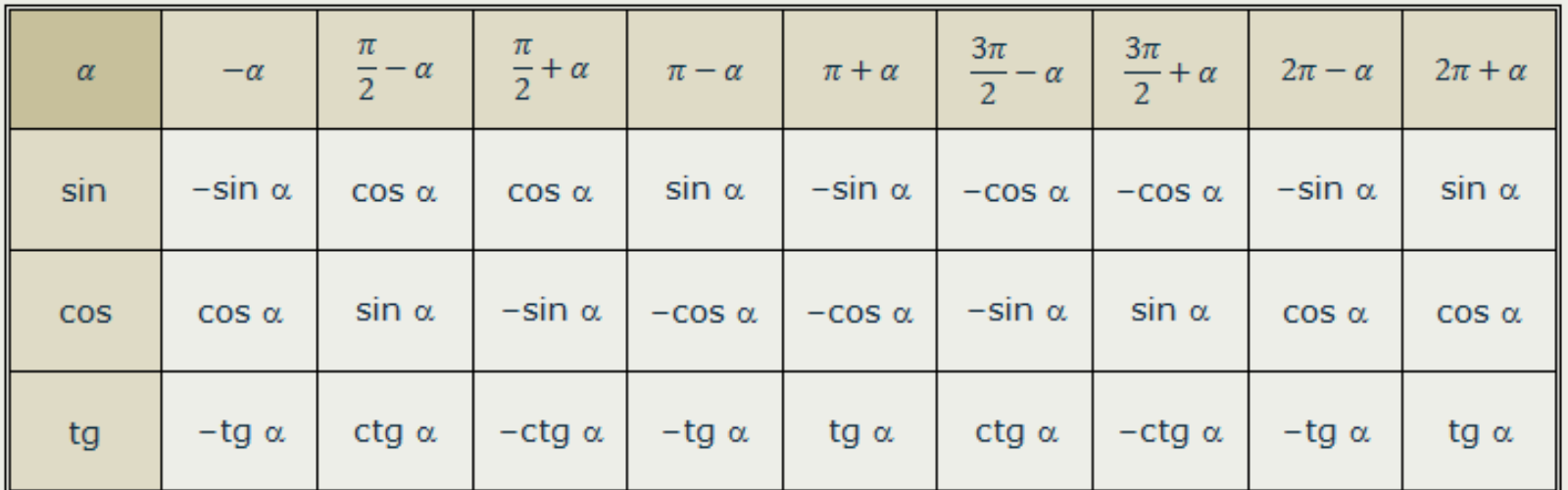
Формулы приведения позволяют тригонометрическую функцию любого произвольного угла выразить через соотношение значений тригонометрических функций известных углов.

Формулы сложения представляют группу формул синуса, косинуса, тангенса суммы и разности углов. Уточнение: косинус, в отличие от остальных функций, является чётной при знаке угла как положительном, так и отрицательном. Нечётность функций предполагает возможность вынесения знака «минус» за знак функции.

Формулы двойного угла основаны на формулах сложения синуса, косинуса, тангенса, котангенса единичных углов. Всё коротко и ясно.
Формулы половинного аргумента в противоположность формулам двойного угла используют значение угла, делённого пополам, в тригонометрических функциях целого угла.

Формулы суммы и разности двух углов рассматриваются как подготовительные для перехода к произведению тригонометрических функций.

Формулы произведения являются базовыми в расчётах. Внимание привлекает сумма и разность косинусов. В силу неизменности знака она не обладает свойством взаимозаменяемости. Знак произведения косинусов зависит от соотношения углов.

Чтобы свободно пользоваться формулами, правильно их применять, их надо выучить. Для вычисления значения тригонометрических функций тригонометрические выражения необходимо упрощать. Для преобразования тригонометрических выражений используются тригонометрические формулы и различные пути их применения: суммирование и вычитание одинаковых слагаемых, вынесение множителя за скобки, умножение и деление на туже величину, введение новых переменных.